CODA: A Noise and Background Reduction Method for Component Detection in Liquid Chromatography/Mass Spectrometry

The CODA algorithm has widespread use in the detection of ‘real’ peaks from noisy MS chromatograms. For example ACD Labs ChromManager and OpenChrom both cite CODA use.  The primary literature reference for CODA is “A Noise and Background Reduction Method for Component Detection in Liquid Chromatography/Mass Spectrometry” and the paper is typical of its type in that it proceeds step-by-step to describe the algorithm interspersed along with examples of its intended use, ie. some before/after examples of MS chromatogram processing & peak identification.

In automated LC/MS peak picking/tracking and identification systems, the CODA algorithm can be leveraged in a way that it can rapidly process large sets of noisy 3D channel data and, using a threshold known as the Mass Chromatogram Quality (MCQ) index value, identify peaks that are more likely to be ‘real’.

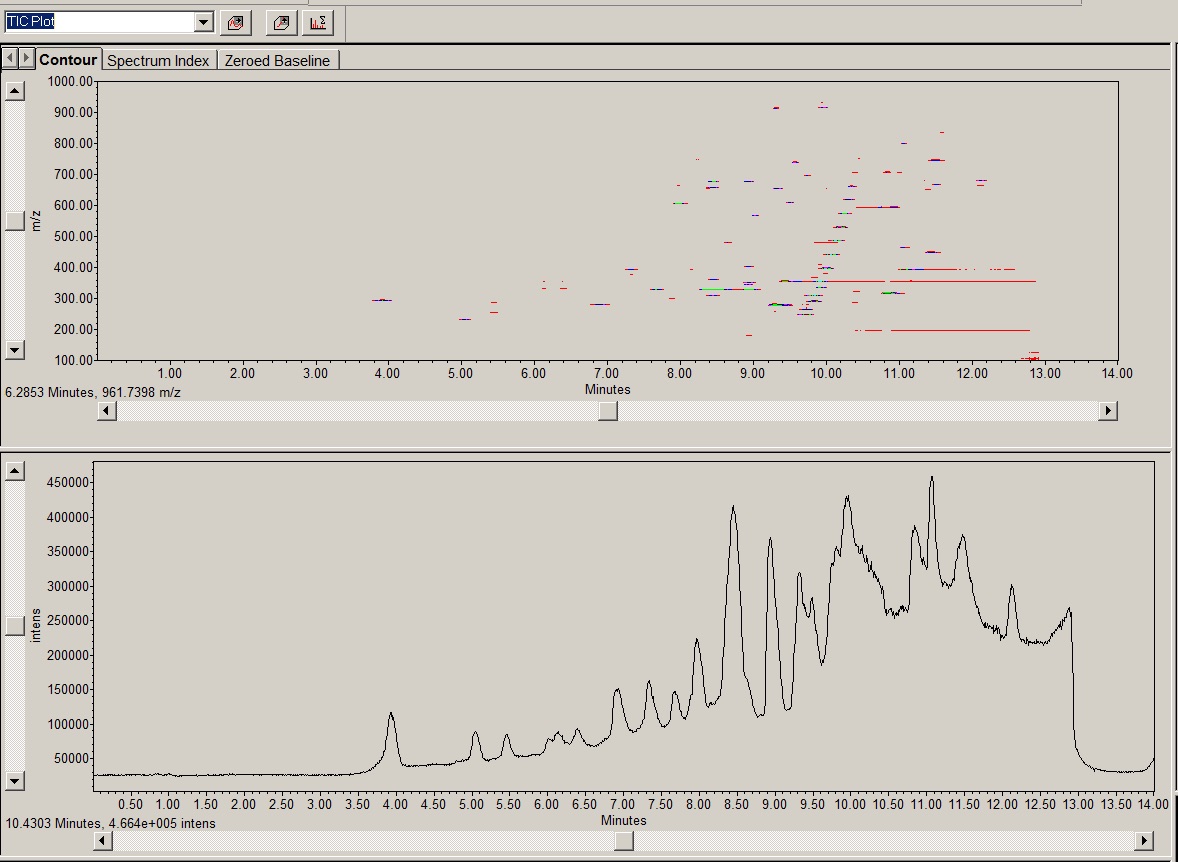
By means of an example, using Waters Empower the TIC for a typical noisy 3D electrospray (+ve) channel is shown below.

From the underlying 3D MS channel data, each EIC can be processed by the algorithm and very quickly it can be demonstrated that there is likely an ionisable component at 529 mass units at around 10.2min (with a very respectable ion count of >30000). The MCQ threshold used for selection threshold criteria was ≥ 0.985. To represent things visually, again using Waters Empower, the EIC slice at 529 mass units is shown in the chromatogram below.

In automated MS peak picking/peak identification processing, where the source 3D MS channel data is available (in the case of Waters Empower, using the Empower toolkit API and some C# code), it is possible to process large sets of 3D MS channel data using algorithms like CODA thereby identifying peaks for closer inspection, eg. 529 as shown above (note I am obviously not saying that there is a component with a nominal mass of 529, just that something [MH+., an adduct or dimer of some sort, a fragmented ion, and so on] has ionised with a mass of 529).

The CODA algorithm described in the Windig paper is written in a step-by-step way for ease of understanding, and not necessarily the most efficient way that it would be coded-up. This poses the same question to me every time – all things being equal should I write source code as the algorithm is implemented in the original citation, or should the source code lends itself to more algorithmic efficiency deviating away from the paper. To reword the prior sentence, if I write source code that follows the original citation, the documentation is the original citation, pages and pages of it, it is clear, it is peer reviewed, and I can limit my code comments to the bare essentials (after all, could I even produce a few useful lines of code comments from the original citation when it contains several thousand words, images, and other citations?).

My C# implementation of the Windig CODA algorithm is shown below:

using System;

namespace uk.co.woodwardinformatics.windig
{
 /// <summary>
 ///  <para>
 ///    Class implementing CODA algorithms as defined in by Willem Windig, J Martin Phalp,
 ///    and Alan W. Payne, "A Noise and Background Reduction Method for Component Detection
 ///    in Liquid Chromatography/Mass Spectroscopy", Anal. Chem. 1996, 68, 3602-3606.
 ///  </para>
 /// </summary>
 public class CODA 
 {
    private const int WINDOWSIZE = 3; // 3, 5, 7, 9, ... boxcar point averaging

    /// <summary>
    ///    Take a matrix and smooth boxcar average it according to the Windig paper reference. 
    ///  <remarks>
    ///    See Windig et al., Anal. Chem. 1996, 68, 3602-3606
    ///  </remarks>
    /// </summary>
    /// <param name="slice1D">
    ///    Matrix to reduce
    /// </param>
    /// <returns>
    ///    Reduced box averaged matrix
    /// </returns>
    private Single[] boxcarSmoothingWindigMatrixReduction(Single[] slice1D)
    {
      Single[] smoothed = new Single[slice1D.Length - WINDOWSIZE + 1];

      for (int i = 0; i < (slice1D.Length - WINDOWSIZE + 1); i++)
      {
        for (int k = 0; k < WINDOWSIZE; k++)
           smoothed[i] += slice1D[i + k];
        smoothed[i] /= WINDOWSIZE;
      }
      return smoothed;
    }


    /// <summary>
    ///    Calculate MCQ from mass spec chromatogram EIC mass slice
    /// </summary>
    /// <param name="chromatogramSlice">
    ///    Single slice
    /// </param>
    /// <returns>
    ///    MCQ as defined in the citation
    /// </returns>
    public Single MCQ(Single[] chromatogramSlice)
    {
      Single codaSimilarityIndex = 0;

      try
      {
        //equation (1) (Euclidean length of chromatogram mass slice), see citation
        Single lambdaJ = 0;
        for (int i = 0; i < chromatogramSlice.Length; i++)
           lambdaJ += Convert.ToSingle(Math.Pow(chromatogramSlice[i], 2));
        lambdaJ = (0 == lambdaJ) ? 1 : Convert.ToSingle(Math.Sqrt(lambdaJ));

        //equation (2), see citation
        Single[] lengthScaledChromatogramSlice = chromatogramSlice.Clone() as Single[];
        for (int i = 0; i < lengthScaledChromatogramSlice.Length; i++)
           lengthScaledChromatogramSlice[i] /= lambdaJ;

        Single[] smoothedReducedStandardizedChromatogramSlice = boxcarSmoothingWindigMatrixReduction(chromatogramSlice);

        //equation (4), see citation
        Single meanJ = 0;
        for (int i = 0; i < smoothedReducedStandardizedChromatogramSlice.Length; i++)
           meanJ += smoothedReducedStandardizedChromatogramSlice[i];
        meanJ /= smoothedReducedStandardizedChromatogramSlice.Length;

        //equation (5), see citation
        Single standardDeviationJ = 0;
        for (int i = 0; i < smoothedReducedStandardizedChromatogramSlice.Length; i++)
           standardDeviationJ += Convert.ToSingle(Math.Pow(smoothedReducedStandardizedChromatogramSlice[i] - meanJ, 2));
        standardDeviationJ /= (smoothedReducedStandardizedChromatogramSlice.Length - 1);
        standardDeviationJ = Convert.ToSingle(Math.Sqrt(standardDeviationJ));

        //equation (3), see citation 
        for (int i = 0; i < smoothedReducedStandardizedChromatogramSlice.Length; i++)
          smoothedReducedStandardizedChromatogramSlice[i] = (smoothedReducedStandardizedChromatogramSlice[i] - meanJ) / standardDeviationJ;

       //equation (9), see citation
       int smoothingWindowCentrePoint = (WINDOWSIZE - 1) / 2;
       for (int i = 0; i < smoothedReducedStandardizedChromatogramSlice.Length; i++)
          codaSimilarityIndex += (smoothedReducedStandardizedChromatogramSlice[i] * lengthScaledChromatogramSlice[i + smoothingWindowCentrePoint]);

       codaSimilarityIndex /= (Single)Math.Sqrt(smoothedReducedStandardizedChromatogramSlice.Length - 1);
      }
      catch
      {
        codaSimilarityIndex = 0f;
      }

      return Single.IsNaN(codaSimilarityIndex) ? 0f : codaSimilarityIndex;
    }
  }
}

Of late, my approach every time now is to defer to the documentation in the primary literature, when I can. Each of the equations referenced in the source code above refer to an equation number in the Windig paper. My source code is clear. The original citation is clear. I believe this is the correct approach for coding up well documented new algorithms, especially as other developers modifying my code may have strengths in other areas – a direct one-to-one mapping of what the code does to the equation number in the original paper can only aid in comprehension &  debugging.

Finally, the way the code above may be used is a) instantiate an instance of the CODA class, b) from the 3D MS data for every mass, extract a 2D EIC slice and invoke the method CODA.MCQ, and in-turn c) compare the calculated MCQ result against your MS quality threshold value making a decision on whether the detected component/peak warrants further investigation.

— Published by Mike, 12:22:18 26 April 2017 (CET)